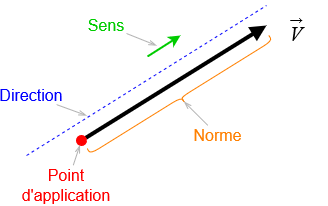
Un vecteur est représenté par un segment orienté (une flèche), ayant pour extrémités un point de départ et un point d’arrivée. L’emplacement dans le plan ou l’espace n’a pas d’importance, deux déplacements de deux points d’origine distincts peuvent correspondre au même vecteur, seuls comptent sa longueur, sa direction et son sens. Il est donc possible de le faire glisser librement dans le plan, parallèlement à lui-même. Si A et B sont deux points distincts, le vecteur A B → 
- sa direction (droite (AB)) ;
- son sens (il y a deux sens possibles de parcours de la droite (AB) : de A vers B ou de B vers A) ;
- sa norme (ou sa longueur, la longueur du segment [AB]).
Attention cependant à ne pas confondre sens et direction. En effet, dans le langage courant, lorsqu’on se trouve sur une route entre Bruxelles et Liège et que l’on dit que l’on va dans la direction de Liège, on se rapproche de cette dernière ville. Mais dans le langage mathématique, la direction est portée par la route (direction Bxl-Liège) sans savoir si l’on va de Liège vers Bxl ou de Bruxelles vers Liège. Pour savoir vers quelle ville on se dirige, il faudra aussi donner le sens : le sens Bruxelles-Liège par exemple pour indiquer que l’on va de Bxl vers Liège.